THEORY
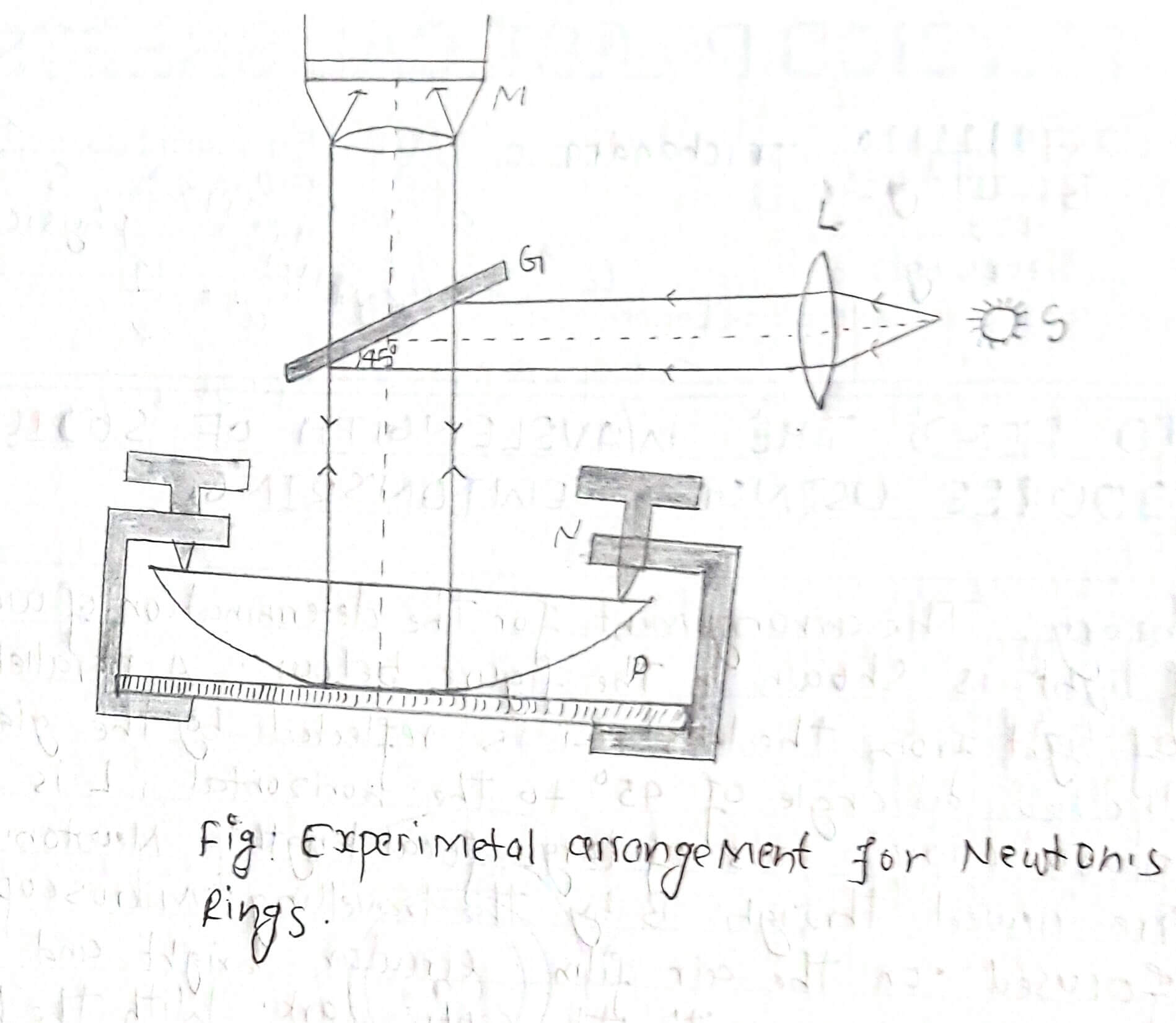
The arrangement for the determination of wavelength of light is shown in the figure below. A parallel beam of light from the lens L, is reflected by the glass plate B inclined at angle of 45° to the horizontal, L is a plano-convex lens of large focal length. Newton’s rings are viewed through B by the traveling microscope M focused on the air film circular bright and dark rings are seen with the center dark. With the help of a traveling Microscope, the diameter is measured for the nth dark ring.
Suppose the diameter of nth ring = Dn
r²n = nλR
but, rn = Dn/2
D2n = 4nλR …………. (i)
The diameter of the (n+m)dark rings is Measured. Let it be Dn+m, Therefore, D2n+m =4(n+m)λR……………(ii)
Substrating (i) from (ii)
D2n+m-D2n = 4(n+m)λR – 4nλR
D2n+m-D2n = 4nλR +4mλR -4nλR
D2n+m-D2n = 4mλR
λ = D2n+m-D2n/4mR ………….(iii)
λ = D2n+m-D2n/4mR
Where
R = Radius of curvature of the surface of lens in content with the glass plate and
Dn = Diameter of nth dark or bright fringes
Dm = Diameter of mth dark or bright fringes
R= l2/6h +h/2
OBSERVATION
l =29mm
h = 0.19mm
R = (29×10-3)2/6X0.19X103 + 0.19X103/2
= 0.68m
| No. of rings | Microscope ReadingLeft (M.S) | Microscope ReadingLeft (C.S) | Microscope ReadingLeft (Total) | Microscope Reading diameter (mm)Right (M.S) | Microscope Reading diameter (mm)right (C.S) | Microscope Reading diameter (mm)right (total) | |
| 20 | 49 | 50 | 49.5 | 43 | 53 | 43.53 | 5.93 |
| 16 | 49 | 83 | 49.83 | 44 | 89 | 44.89 | 4.94 |
| 12 | 48 | 54 | 48.54 | 44 | 23 | 44.23 | 4.31 |
| 8 | 48 | 67 | 48.67 | 45 | 0.4 | 45.04 | 3.63 |
| 4 | 48 | 18 | 48.18 | 45 | 59 | 45.59 | 2.59 |
| (m,n) | ( D2n- D2m) (10-6m2) | λ = D2n- D2m/4R(n-m) (10-7m) |
| (12,16) | 5.8275×10-6m2 | 5.356×10-7m |
| (12,8) | 5.3992×10-6m2 | 4.9×110-7m |
| (8,4) | 6.4688×10-6m2 | 5.946×10-7m |
| (20,16) | 10.76×10-6m2 | 9.8×10-7m |
CALCULATION
Mean of wavelength (λ)= (5.356 +4.9 +5.946 +9.8)X10–7 / 4
= 26/4 x10-7m
= 6.5×10-7m
ERROR= (Standard value – Observed value)/Standard value x 100%
= (5890-6500 / 5890 x 100)
= 610 X 100 / 5890
= 10.356%
RESULT
The wavelength of given sodium light by using Newton’s ring is found to be 6.5X10-7m with error 10.356%
PRECAUTIONS
i) A lens and glass plate should be cleaned.
ii) A lens of Large Radius of curvature preferable plane convex should be used.
