To Determine The Modulus Of Rigidity of Given Wire Using Maxwell’s Needle.

APPARATUS REQUIRED

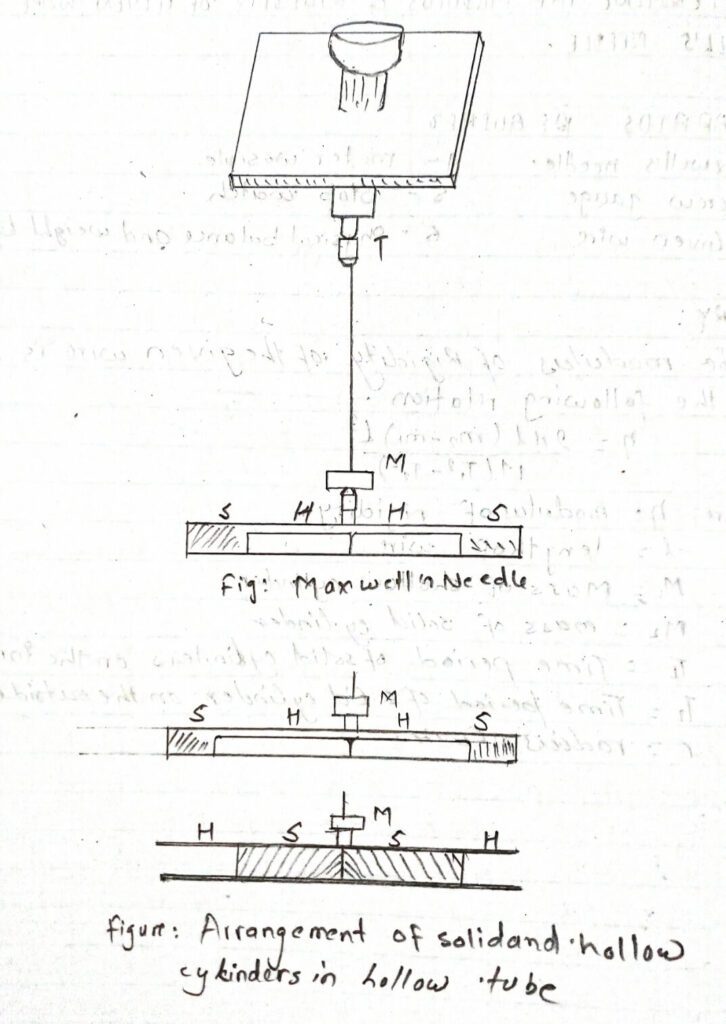
i) Maxwell’s needle.

ii) Screw gauge

iii) Meter scale

iv) Stopwatch

v) Given wire

vi) Physical balance and weight box.

THEORY:

The modulus of Rigidity of the given wire is calculated by the following relation.

η = 2πl(m₂-m₁) l³ / r⁴(T²₁-T²₂)

Where, η = modulus of rigidity.

 l= length of wire

M₁ = Mass of hollow cylinder

M₂ = mass of solid cylinder

T₁ = Time period of solid cylinders on the innerside

T₂ = Time period of solid cylinder on the outside

r= radius of wire

OBSERVATION: 

Table for determination of T₁ and T₂

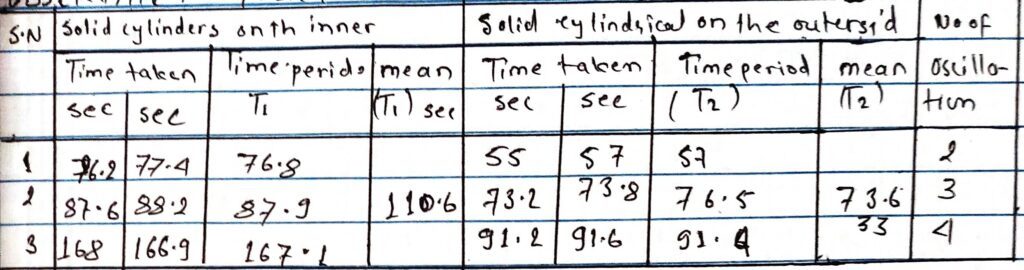
length of wire (l) =79cm     =0.79m

length of maxwell’s needle (l) = (0.41) m

Mass of hollow cylinder (M₁) = 50 gm  = 0.05kg

Mass of solid cylinder (M₂) = 250gm     = 0.25kg

Radius of wire (r) = 45×10^-5/2 m

CALCULATION

Modulus of rigidity (η) : 2π(m₂-m₁)l² / r⁴(T²₁-T²₂)

= 2π(0.25 -0.05) (0.41)² / (45X10^-5/2)⁴ [(110.6)²-(73.633)²]

= 9.40×10⁹ N/m²

PERCENTAGE ERROR

Standard value 7η = 1.7 × 10¹¹ N/m²

observative value (η) = 9.4×10⁹ N/m²

Here error = Standard value-observative value /  Standard value X100%

= 94.5%

RESULT:

Thus the modulus of rigidity of the given wire was found to be 1.40X 10⁹ N/m²

CONCLUSION

Thus the modulus of rigidity of the given wire can be determined by using Maxwell’s needle.