TO DETERMINE THE Modulus of RIGIDITY OF GIVEN WIRE BY TORSIONAL PENDULUM

APPARATUS REQUIRED

i) Given wire

ii) Stop watch

iii) Vernier calipers

iv) Physical balance weight box

v) A right circular cylinder

THEORY

The torsional pendulum consists of a rigid heavy circular cylinder of known moment of inertia I, about an axis through its center of gravity fixed at the lower end of the given experiment at wire such that the axis of wire passes through the center of gravity.

If ‘T’ is the time-period of torsional vibration of the system and ‘C’ the couple per unit angular twist of the wire then, 

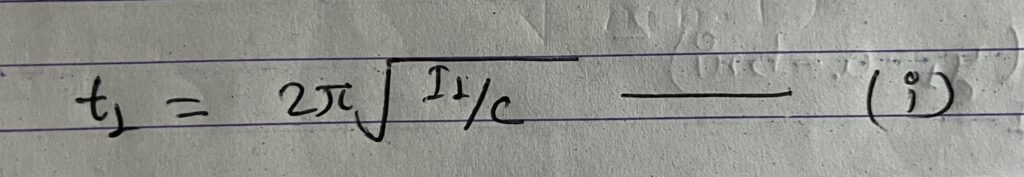
Similarly, if another body with moment of inertia I2 about an axis through center of gravity is placed along with the circular cylinder and the time period t2 of the system is found out them.

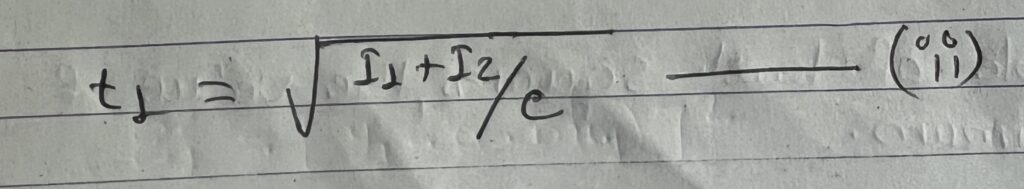
Squaring and dividing on both side on equation (i) and (ii)

t²₁/t²₂ = I₁/I₁+I₂

I₁ +I₂ = t²₂/t²₁ x I₁

I₂ = I₁. T²₂/T²₁ – I

The moment of inertia of the cylinder is given by I₁= 1/2 x mr² where m is the mass of the cylinder and r is radius of the cylinder.

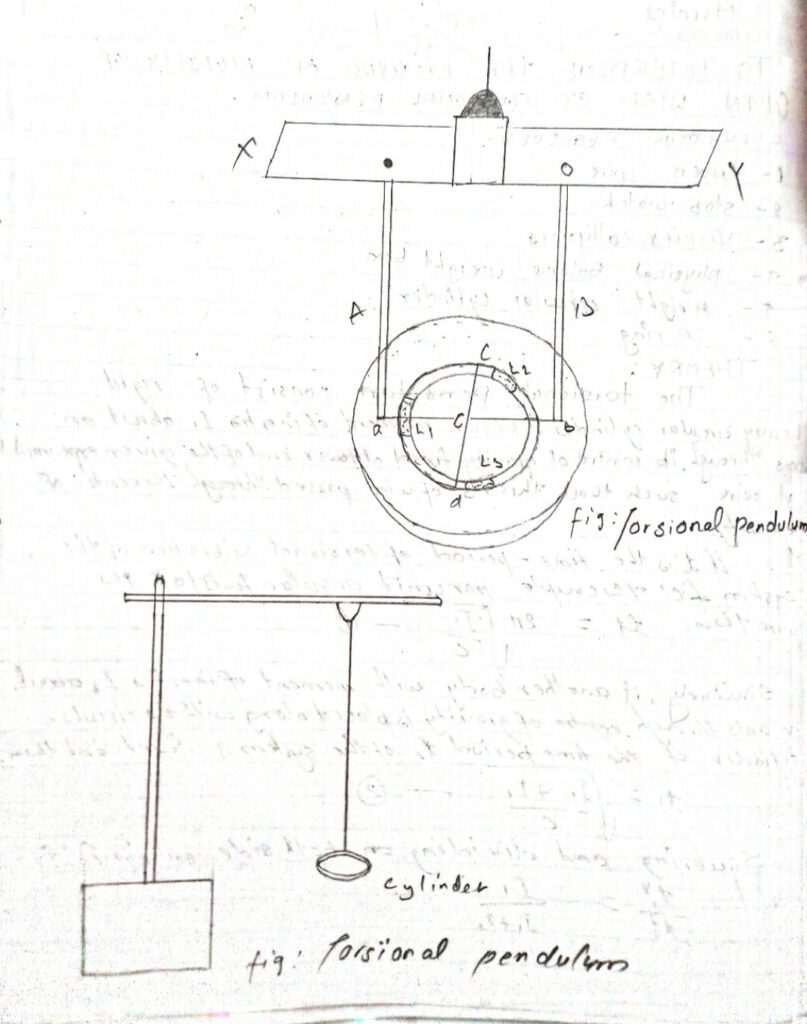
PROCEDURE

i) The measured diameter in a solid cylinder with the help of vernier calipers along two mutually perpendicular directions and then calculate the radius of the cylinder.

ii) Again calculate the mass of the cylinders with the help of a physical balance.

OBSERVATION

for the 20 oscillations.

S.N	Time period	Mean time
1	3.34
2	3.32
3	3.29	3.296
4	3.27
5	3.26

CALCULATION

length of wire (l) = 79cm

Mass of caliper(m) = 91.5m

Radius of wire (r) = d/2 = 1.64×10⁴ =0.73mm

Moment of inertia (i) = mr²/2 = 91.5 x (0.73)² / 2

= 24.38

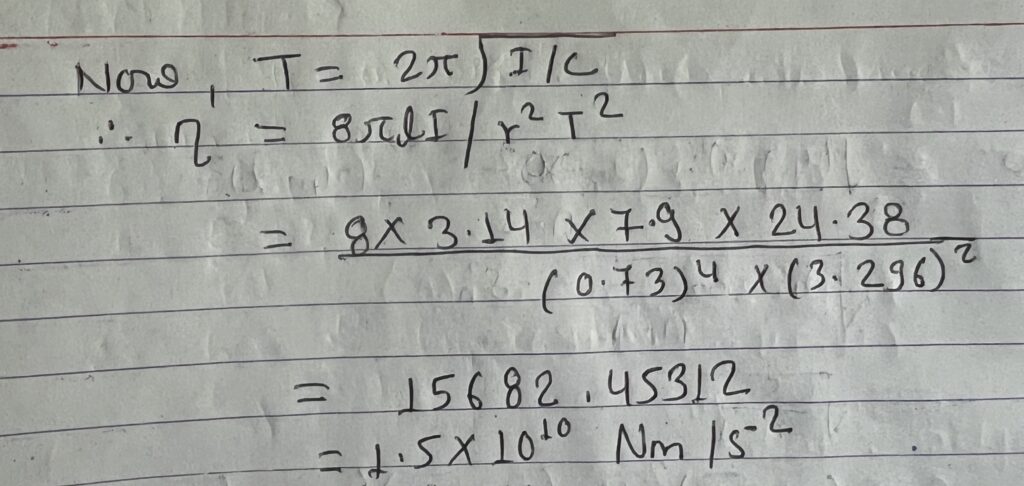
PERCENTAGE OF ERROR

Standard value of η = 8.9×10¹⁰-7.5×10¹⁰/8.9×10¹⁰ x 100

= 83.14%

RESULT

Thus, the modulus of Rigidity of the given wire 12 found 1.5×10¹⁰ Nm/s²