APPARATUS REQUIRED
i) A Flywheel
ii) A strong and thin string
iii) Vernier calipers
iv) Stopwatch
v) Different mass
vi) Apice of chalk
THEORY
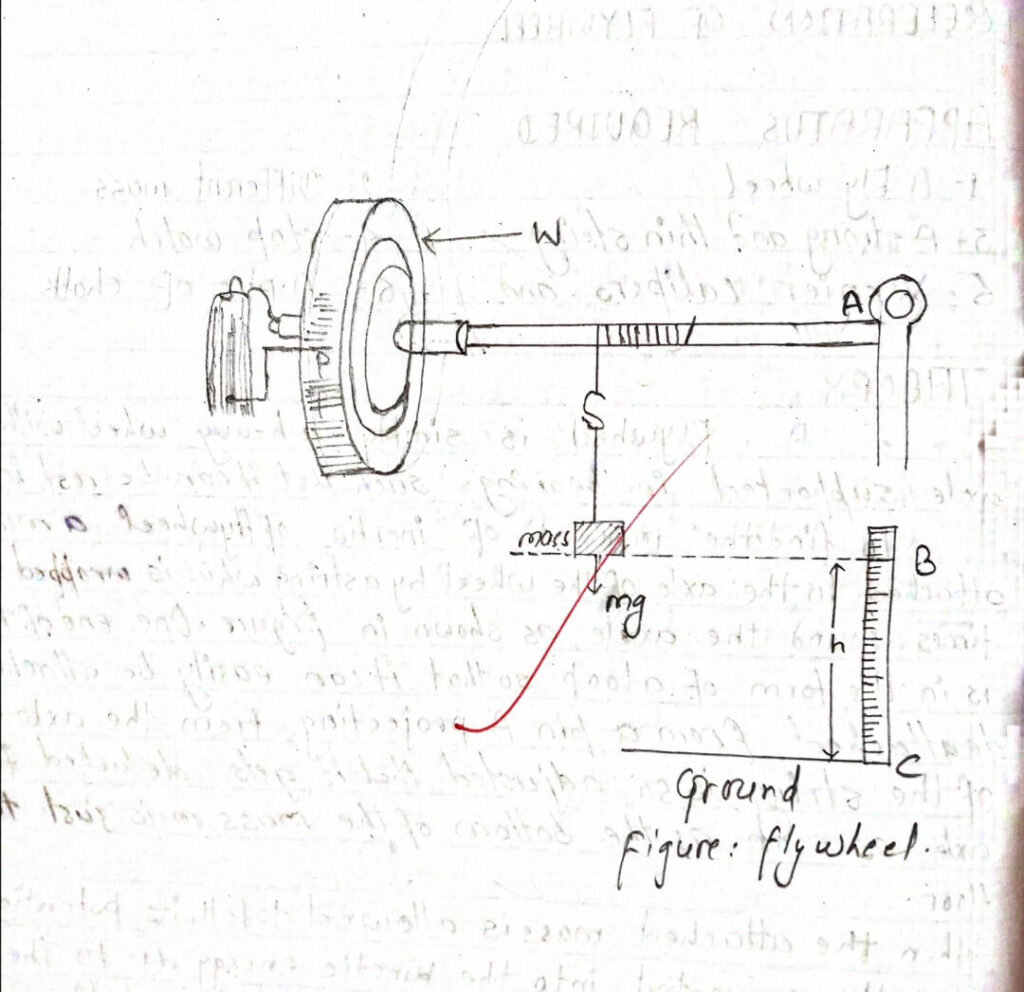
A Flywheel is simply a heavy wheel with a long axle supported in bearing such that it can be rest in any position.
To find the moment of inertia of a flywheel a mass ‘m’ is attached to the axle of the wheel by a string which is wrapped several times around the axle as shown in Figure. One end of the string
is in the form of a loop so that it can easily be attached to or detached from a pin A projecting from the axle. The length of the string is so adjusted that it gets detached from the axle as soon as the bottom of the mass ‘m’ is just to touch the floor.
When the attached mass is allowed to fall, its potential energy is partly converted into the kinetic energy due to the velocity gained by it and partly into the energy of rotation of the flywheel.
let, ‘w’ be the angular velocity gained by the wheel at the moment the mass ‘m’ is detached.
After the string has been detached from the wheel, the wheel revolves for some time continuously. Its angular velocity decreases due to friction and finally the wheel comes to rest. If n, is the number of revolutions that the wheel makes in time ‘t’ before coming to rest. then,
Average angular velocity = 2πn1/t
If the frictional force is constant the rotation of the wheel is uniformly slowed down. It starts with an angular velocity w and its final angular velocity is zero, so that the initial velocity w is double the average velocity. or, w = 2x 2πn1/t = 4πn1/t
According to the principle of conservation of energy, when the string is detached.
P.E. of mass m = K.E of m + K.E of wheel + Work done against friction. Where, P.E of mass m=mgh, ‘h’ is the height through which the mass has fallen.
If ‘r’ is the radius of the axle, then,
linear velocity of mass m1 = rw
and K.E of mass m = 1/2 m (rw)²
If ‘I’ is the moment of inertia of the wheel, then K.E of the wheel = 1/2 IW2
Let ‘f’ be the energy per revolution used in overcoming the frictional force. If n is the number of revolutions the wheel makes during the descent of the mass m. then,
Total energy used to overcome friction =nf
Hence, mgh = 1/2 mr² w² + 1/2 Iw² + nf
The kinetic energy possessed by the wheel is used up in overcoming friction. As the wheel comes to rest after making a revolution. Therefore, n1f = 1/2 Iw2 or, F= 1/n1 1/2 Iw2
Substituting, the value off is above equation, we have
mgh= 1/2mr2w2 +1/2Iw2. 1+n/n1
I= 2mgh-mr2w2/w2 1+n/n1
This relation gives the moment of inertia of the flywheel.
PROCEDURE
i) Check the wheel and see that there is the least possible friction. Oil the bearings, if necessary.
ii) Measure the diameter of the axle with vernier calipers at different points and find the mean. Determine circumference of wheel ‘w’ with a thread.
iii) Repeat the experiment with three different masses, adjusting the height through which the mass falls so that the number of rotations made by the wheel can be easily noted.
OBSERVATIONS
Vernier constant (V.C) = 0.01 cm
Diameter of the axle = i) 2.16cm ii) 2.19cm iii) 2.12cm
Mean diameter of the axle =2.16cm
Therefore, radius of the axle (r) = 1.066cm
Circumference of the flywheel (s) = 76cm
Height (h) = 107 cm, Mass (m) = m1=1500gm, M2 = 250gm, M3=350gm
No.of turns wounded on axle (r) = 15
Acceleration due to gravity (g) = 10ms-2
Table-1
| S.N | Mass (gm) | No.of complete revolution made by the wheel(a) | Distance of chal R market from the pointed(d) | Fraction of revolution (d/r)=b | No.of revolution n1= a+b | Time(sec) |
| 1 | m1=150 | 26 | 12.5 | 12.5/76=0.16 | 26.16cm | 64 |
| 2 | m2=250 | 43 | 56 | 56/76=0.74 | 43.74 | 81 |
| 3 | m3=350 | 64 | 48 | 48/76=0.63 | 64.63 | 98 |
Table-2
| S.N. | Main scale Reading ‘a’ | Vernier scale reading | Vernier scale reading | a+b | Mean |
| 1 | 2.1 | 6 | 0x0.01=0.06 | 2.16 | 2.1367 |
| 2 | 2.1 | 3 | 3×0.01=0.03 | 2.13 | |
| 3 | 2.1 | 2 | 2×0.01=0.02 | 2.12 |
Angular velocity of 1st
CALCULATION


RESULT
From the above experiment we found moment of inertia to be 824778.47 gmn2 and angular acceleration 2.87×10-2 rads-1
CONCLUSION
In This way the moment of inertia and angular acceleration was found with error 0.03%.
PRECAUTION
i) There should be the least possible friction in the flywheel.
ii) The strip should be thin and should be found.
iii) The stop watch should be startech just when the string detaches.
iv) The loop slipped over the pin should be chosen enough so that it comes easily.
