APPARATUS REQUIRED
i) Steel ball
ii) Micrometer Screw gauge
THEORY
The precision with which a physical quantity is measured depends inversely upon the deviation or dispersion of the set of measured values x1 about their mean value x̄. If the values are widly dispersed the precision is said to below.
The deviation δ1 = x1 – x̄
Average deviation:
The average value of the deviation of all the individual measurements from the arithmetic mean is known as average deviation and is denoted by d ¯
Therefore, d ¯ = (x1-x̄) + (x2-x̄)…………+ (xn-x̄) / n
= δ1 + δ2 +………… δn / n
= Σ δi / n
Standard deviation:
The square root of the mean square deviations of an infinite set of measurements is known as standard deviation and is donated by σ. The number of observations is sufficiently large.
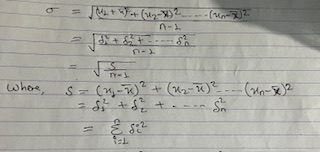
For a fairly large sample of measurements which have reasonable normal distribution about the mean value x̄.
ஃ Average deviation/standard deviation = d ¯/σ = 0.80.
Standard error:
The quantity of σ/√n is known as standard error and denoted by σM
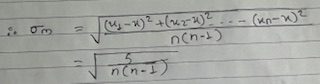
from a finite number of observations n may be the internal μ ± . σM is 0.68 that it may lie between 0.95 and for 0.99.
Probable error:
The probable error is a quantity such that there is an even chance whether the true value for the quantity measured differs from the mean value by an amount greater or less there.
Probable error = ± 0.6745 √s / n(n-1)
= ± 0.6745 standar error
OBSERVATION TABLE:
| no. of obs. | Radius of curvature | δ | δ2 |
| 1 | 15.25 | 0.07 | 0.0049 |
| 2 | 15.42 | +0.10 | 0.0100 |
| 3 | 15.30 | -0.02 | 0.0004 |
| 4 | 15.20 | -0.12 | 0.0144 |
| 5 | 15.35 | +0.03 | 0.0009 |
| 6 | 15.40 | +0.08 | 0.0064 |
Mean radius of curvature = 15.32
S = δ21 +δ22 +δ23 +δ24 +δ25 +δ26
= 0.049+0·0100 +0.0004 +0.0144 +0.0009+0.0064
= 0.0370
a) Average deviation d ¯ = δ1+δ2+δ3+δ4+δ5+δ6
= 0.07 +0.10 -0.02 +0.03 +0.08 -0·12 / 6
= 0.14/6
= 0.02333
b) Standard deviation σ = √S/n-1
= √0.0370/6-1
= 0.0860
c) Standard error σM = S/ n(n-1)
= √0.0370/6(6-1)
= √0.0370/30
= 0.03512
d)Probable error = ± 0.6745× standard error
= ± 0.6745×0.03512
= ± 0.0237
Radius of curvature = 15.32 ± 0.0237
RESULT:
Average deviation of steel ball = 0.02333
Standard deviation of steel ball = 0.0860
Standard error of steel ball = 0.03572
finally probable error of steel ball 12 ± 0.0237
